Putting Predictor
April 2024
I have noticed that the "perfect line" calculators in golf games such as EA's PGA Tour are terrible - they are remarkably slow, often taking nearly 30 seconds on gaming hardware just to fail to find a line. To me, this seems like quite a simple numerical problem so I decided to make my own.
Generating the surface
The putting surface is generated with a sum of sine functions, at different amplitudes, frequencies and phase shifts. This gives a natural feeling surface, is a good challenge for the simulator and also makes for a quick and simple calculation of heights and partial derivatives at any point using the chain rule. The mathematical shape was also not exploited for the alignment algorithm, as the idea is that the algorithm works across any surface.
Generating the surface
public float getHeightAtPos(float x, float z)
{
float dsp = 0f;
for (int i = 0; i < degree; i++)
{
dsp += xAmplifiers[i] * MathF.Sin(((x / cellSize) / xStretches[i]) - xShifts[i]);
dsp += zAmplifiers[i] * MathF.Sin(((z / cellSize) / zStretches[i]) - zShifts[i]);
}
return dsp;
}
public float getXPartialAtPoint(float x)
{
float pd = 0;
if (x < height / cellSize && x > 0)
{
for (int i = 0; i < degree; i++)
{
pd += xAmplifiers[i] / xStretches[i] * MathF.Cos(((x / cellSize) / xStretches[i]) - xShifts[i]);
}
}
else
{
pd = x > 0 ? 1f : -1f;
}
return pd / cellSize;
}
public float getZPartialAtPoint(float z)
{
float pd = 0;
if (z < height / cellSize && z > 0)
{
for (int i = 0; i < degree; i++)
{
pd += zAmplifiers[i] / zStretches[i] * MathF.Cos(((z / cellSize) / zStretches[i]) - zShifts[i]);
}
}
else
{
pd = z > 0 ? 1f : -1f;
}
return pd / cellSize;
}

Brute force
Aimlessly simulating all trajectories in the vague direction of the hole worked very well, but obviously wasn't very efficient.

Brute force
public void bruteForce()
{
float bd = Mathf.Atan2((green.flagPosition.x - b.transform.position.x), (green.flagPosition.z - b.transform.position.z)) * Mathf.Rad2Deg;
dir.direction = bd;
Vector3 spos = b.transform.position;
int pointCount = 0;
for (int j = 1; j < 5; j++)
{
List possibilities = new List(); ;
List[] positions = new List[160 * j];
for (int p = 3; p < 30; p += 3)
{
int[] pc = new int[160 * j];
for (int d = 0; d < 160 * j; d++)
{
float dr = (d * (0.5f / j) * (d % 2 == 0 ? -1f : 1f)) + bd;
positions[d] = new List();
positions[d].Add(spos);
Vector3 pos = spos;
float pdX = green.getXPartialAtPoint(pos.x);
float pdZ = green.getZPartialAtPoint(pos.z);
Vector3 vel = new Vector3(Mathf.Sin(dr * Mathf.Deg2Rad), 0, Mathf.Cos(dr * Mathf.Deg2Rad)) * (float)p;
Vector3 accel = Vector3.zero;
int i;
for (i = 0; i < lengthGuide * resolutionGuide; i++)
{
pdX = green.getXPartialAtPoint(pos.x);
pdZ = green.getZPartialAtPoint(pos.z);
accel = new Vector3(-pdX * b.gravity, 0, -pdZ * b.gravity);
Vector3 velocityDirection = Vector3.Normalize(vel);
Vector3 frictionAcceleration = -velocityDirection * b.friction * b.gravity;
vel += (accel + frictionAcceleration) * (1f / resolutionGuide);
pos += vel * (1f / resolutionGuide);
pos = new Vector3(pos.x, green.getHeightAtPos(pos.x, pos.z) + 0.1f, pos.z);
positions[d].Add(pos);
pc[d]++;
float distance = Vector3.Distance(new Vector3(pos.x, pos.z), new Vector3(green.flagPosition.x, green.flagPosition.z));
if (distance < 0.1f)
{
hasSuccess = true;
possibilities.Add(d);
break;
}
if ((accel + frictionAcceleration).magnitude * (1f / resolutionGuide) < 0.02f && vel.magnitude * (1f / resolutionGuide) < 0.02f)
{
break;
}
}
}
pointCount += pc.Sum();
if (possibilities.Count() > 0)
{
int fewestPositions = 1000000000;
int fewestIndex = 0;
for (int a = 0; a < possibilities.Count; a++)
{
if (positions[possibilities[a]].Count < fewestPositions)
{
fewestIndex = a;
}
}
int f = possibilities[fewestIndex];
lr2.positionCount = positions[f].Count();
lr2.SetPositions(positions[f].ToArray());
perfectPower = p;
perfectAngle = (f * (0.5f / j) * (f % 2 == 0 ? -1f : 1f)) + bd;
return;
}
}
}
}
The next approach was an adaptation of this. The shot power was increased until the ball was able, when aimed directly at the hole, to reach the edge of the vertical cylinder around it's starting position o with the radius of the distance from o to the hole. This method of first finding an acceptable power is closer to what is used in golf games.
Then, many trajectories are simulated and when two are found that encompass the hole, that angle range is subdivided and shots are simulated from within there. This is repeated until a successful trajectory is found. This was by far the best method.

Starting from the flag
Next, I tried the other way round - initialising with the ball at the flag, and running the simulation backwards with different entrance trajectories. This allowed for a set entrance speed, which is impossible to account for in the other methods whilst keeping efficiency.
I used a similar vertical cylinder with the same radius as before, but this time centered around the hole. The angle formed upon intersection with the cylinder when simulating backwards was recorded, and gradient descent with Newton-Raphson step size was applied to adjust the entrance angle.
Backwards finding
public IEnumerator find(float startAngle)
{
float startTime = Time.realtimeSinceStartup;
float angleToTry = startAngle;
float prevAngle = startAngle;
var output = backwardSim(angleToTry);
float f_current = output.Item1;
float f_prev = f_current;
float step = 0.5f;
for (int i = 0; i < 100; i++)
{
yield return new WaitForSeconds(0.05f);
float denominator = f_current - f_prev;
float newAngle;
if (MathF.Abs(denominator) > 1e-6f)
{
newAngle = angleToTry - (f_current * (angleToTry - prevAngle) / denominator) * step;
newAngle += 0.01f * (newAngle - prevAngle);
}
else
{
newAngle = angleToTry + 0.1f;
}
prevAngle = angleToTry;
f_prev = f_current;
angleToTry = newAngle;
output = backwardSim(angleToTry);
if (output.Item4)
{
endVel *= 1.5f;
continue;
}
f_current = output.Item1;
if (Vector3.Distance(output.Item2[0], b.transform.position) < 0.1f)
{
hasSuccess = true;
perfectAngle = 0;
perfectPower = 0;
for (int j = 0; j < output.Item3.Length; j++)
{
perfectAngle += MathF.Atan2(output.Item3[j].x, output.Item3[j].z) * Mathf.Rad2Deg;
perfectPower += output.Item3[j].magnitude;
}
perfectAngle /= output.Item3.Length;
perfectPower /= output.Item3.Length;
dir.power = perfectPower;
dir.direction = perfectAngle;
break;
}
else if (f_current < 0.03f)
{
step = 0.1f;
}
}
}
public (float, List, Vector3[], bool) backwardSim(float entrance)
{
Vector3 holePos = green.flagPosition;
Vector3 startPos = b.transform.position;
List positions = new List();
positions.Add(holePos);
Vector3 pos = new Vector3(holePos.x, 0, holePos.z);
float pdX = green.getXPartialAtPoint(pos.x);
float pdZ = green.getZPartialAtPoint(pos.z);
Vector3 vel = surfaceDir(pos, entrance) * endVel;
Queue vels = new Queue();
while (true)
{
pdX = green.getXPartialAtPoint(pos.x);
pdZ = green.getZPartialAtPoint(pos.z);
Vector3 accel = new Vector3(-pdX * b.gravity, 0, -pdZ * b.gravity);
Vector3 frictionAccel = -vel.normalized * b.friction * b.gravity;
Vector3 _v = vel - (accel + frictionAccel) * step;
pos -= _v * step;
if (Vector3.Distance(xz(pos), xz(startPos)) > Vector3.Distance(xz(positions[positions.Count - 1]), xz(startPos)) && Vector3.Distance(pos, xz(holePos)) > Vector3.Distance(xz(startPos), xz(holePos)) * 1.0f)
{
break;
}
vel = _v;
vels.Enqueue(vel);
if (vels.Count > 1) { vels.Dequeue(); }
positions.Add(new Vector3(pos.x, green.getHeightAtPos(pos.x, pos.z) + 0.05f, pos.z));
if ((vel.sqrMagnitude <= 0.1f * step * step))
{
return (0, new List(), new Vector3[0], true);
}
else if (Vector3.Distance(xz(pos), xz(holePos)) >= Vector3.Distance(xz(startPos), xz(holePos)) * 1.2f)
{
break;
}
}
positions.Reverse();
Vector3 alpha = holePos - startPos;
Vector3 beta = holePos - positions[0];
float angle = MathF.Acos(Vector3.Dot(alpha, beta) / (alpha.magnitude * beta.magnitude));
return (angle, positions, vels.ToArray(), false);
}
public Vector3 surfaceDir(Vector3 pos, float angle)
{
float pdX = green.getXPartialAtPoint(pos.x);
float pdZ = green.getZPartialAtPoint(pos.z);
Vector3 normal = new Vector3(-pdX, 1f, -pdZ).normalized;
Vector3 horizontalDir = new Vector3(Mathf.Sin(angle), 0f, Mathf.Cos(angle));
Vector3 tangentDir = horizontalDir - Vector3.Dot(horizontalDir, normal) * normal;
return tangentDir.normalized;
}
There are several problems with this method. Most of them stem from the discrepancy between simulating forwards and backwards; the acceleration based on the angle of the slope is calculated exactly one step offset from where it should be. The ball should move from it's position based on the nature of the position it is in, rather than the nature of the position it (may) move to.
This is obvious in the frequent misalignment between the green and blue traces in the simulation.
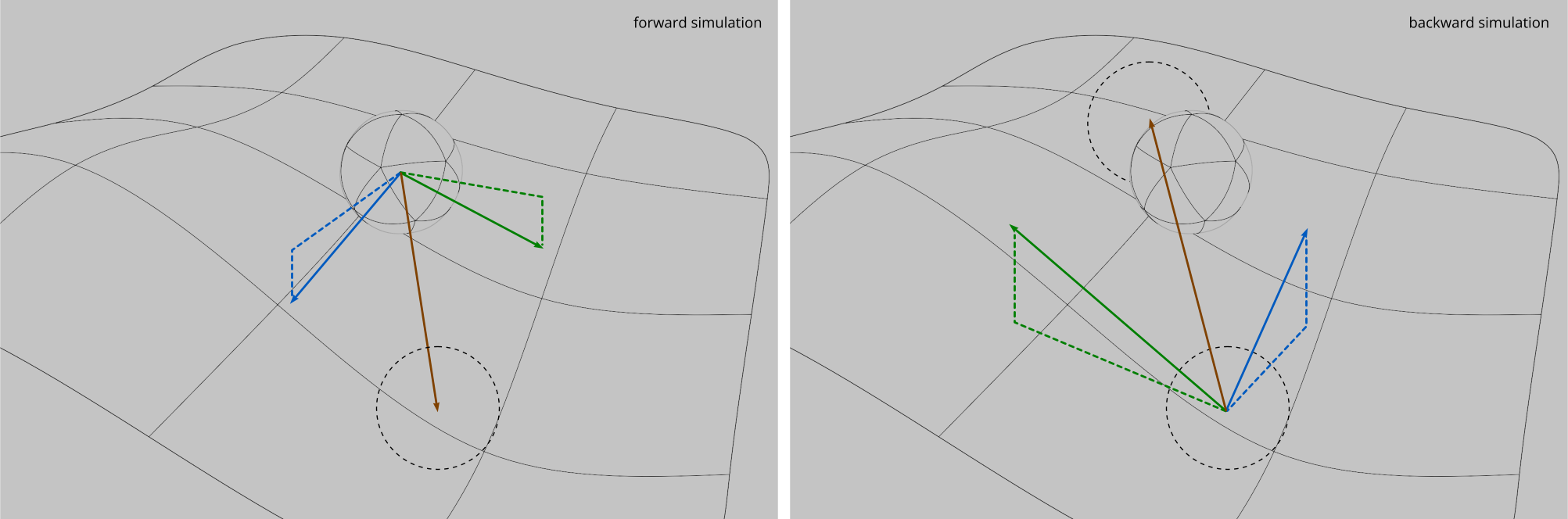
Below is the backward simulation. The WebGL build seems to have introduced several bugs, and decreased the runtime speed dramatically. The lower frame-rates also decrease the accuracy, as the ball moves one simulation step per frame after being fired.